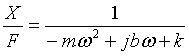..................(2)This experiment has dual objectives. First, it is a classic experiment in characterizing the dynamic response of a system. In this case the response is a simple structure, described by theoretical methods of the type you have studied previously in mechanics of materials, vibration and controls courses. Second, this experiment involves a typical application of analog electronic instrumentation. It is also an experiment that is well suited to digital measurement, analysis and control.
You are expected to perform this experiment as you would any of the other experiments in the course. Specifically, you will need to:
Carefully read this chapter of the manual.
Meet with the other members of the team in advance to plan for the experiment, and open a logbook to record your preparation. You will be required to submit this logbook through CANVAS the day before your perform this experiment.
During the experiment you complete the logbook with your experiences, the data you collected, the analysis performed and conclusions drawn. The completed logbook is due through CANVAS by the end of your session.
The following notation defines the properties of this structure:
kb = 12EI / L3 and μ = 156 / 420 = 0.371
The equation for kb can be obtained directly from the standard beam element stiffness matrix (Megson, p. 458), or by applying the method described in Section 8.4 of Beer and Johnston. The value for μ is an accurate approximation derived from advanced beam theory (Meirovitch, pp. 309-310). Since beam mass is small compared with M in this experiment, the value of μ will have only a small effect.
We can now write the equation of motion for the laboratory structure. As a simple linear system, the equation of motion of the mass, under the action of a fluctuating force f(t) should be:
mẍ+bẋ+kx = f(t)..................(1)
where, in this case, the total mass m will be the sum of the rigid mass and the contributions from the two beams (m = M + 2μρbL), the total damping, b, will be that due to the dashpot plus that inherent in the system, and the total spring constant, k, will be the sum of the constants for the two beams (k = 2kb). Note that the representation of damping in Equation 1 is approximate, since it assumes ideal viscous damping (force proportional to velocity). The inherent damping of this laboratory structure is very small, so that almost all of the damping you will observe is caused by the dashpot (Figure 2). In the experiment an electromechanical shaker will be used to exert a sinusoidal excitation force f(t) onto the mass at the end of the beam, as shown in Figure 1. Note that the shaker is not exerting the force and the beam tip, where the mass is mounted, but rather near the root of the beam. This minimzes the potential contamination of the shaker's own internal stiffness in the beam system. However, Equation 1 assumes that the force is measured at the mass. You will therefore need to use beam theory to convert the force measurements at the root to what they should be at the beam tip. A proximitor (a non-contact position sensor) will then be available to measure the resulting translation of the mass x(t), as also shown in Figure 3.
Solution to the equation of motion for sinusoidal fluctuations.
The behavior of the structure, characterized by the relationship between
forcing, f(t), and the displacement it produces, x(t), is of course
given by the solution to Equation 1. One way to obtain this is by Laplace
transform (see Ogata, Example 7-2). An alternative route, that explicitly
recognizes our interest in the response of the structure to different
frequencies of forcing, is to assume a sinusoidally fluctuating force and (since
the system is linear) a corresponding sinusoidally fluctuating response. Adding
a fictitious imaginary part we write
f(t) = F(ω)e jωt
x(t) = X(ω)e jωt
where w is the angular frequency of the sinusoidal fluctuation. F(w) and X(w) are complex numbers whose magnitude represents the amplitude of the force or displacement fluctuation, and whose argument (angle) represents the phase of that fluctuation. We note that,
ẋ(t)=jωX e jωt
ẍ(t)=-ω2X e jωt
Substituting into Equation 1 we thus obtain
-mω2X e jωt + jbωX e jωt + kX e jωt = F e jωt
Canceling e jωt we obtain,
-mω2X + jbωX + kX = F
and thus
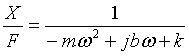..................(2)
So, the ratio between the amplitude of the displacement, xm, and the amplitude of the force that produces it, fm, at angular frequency, w, is
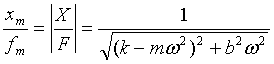..................(3)
referred to as the dynamic flexibility. The phase lag, ym, between the displacement fluctuations and the force fluctuations producing them at angular frequency, w, is
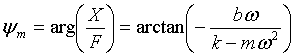..................(4)
We can summarize these results as indicating that, with the mass excited by a sinusoidal force, f(t) = fmsin(ωt), the solution for the steady-state sinusoidal displacement of the mass is, x(t) = xmsin(ωt+ψm). It is worth making some observations here:
a) The dynamic flexibility (Equation 3) at zero or very low frequency is simply 1/k. This is termed the static flexibility.
b)
If the system were undamped (b=0), the dynamic flexibility,
Equation 3, would become infinite when k = mw
2, in other words when the frequency,
.
This is termed the natural frequency of the system and given
the symbol, wn.
c)
The dynamic flexibility peaks when the denominator of Equation 3 is at a
minimum. This condition is called resonance. The resonant frequency,
,is close to the natural frequency for light damping.
d) At the natural frequency the phase response of the actual damped system (b > 0), is -90 degrees, regardless of the damping.
e)
At the natural frequency the dynamic flexibility of the actual damped
system is given by, 
. Dividing this by the static flexibility, 1/k, we obtain
a ratio of, 
. This defines the parameter,
z, referred to as the viscous
damping factor.
f) At frequencies much larger than the natural frequency the dynamic flexibility varies as 1/(mw 2), and the phase response as tanym = b/(mw). Thus, when plotted on a log-log scale the dynamic flexibility tends to slope of -2 at high frequency, and tanym tends to a slope of -1.
g) At frequencies well below the natural frequency, the phase (in radians) varies with frequency linearly, as tanym = -bw/k.
h) The phase is always between 0 and -p.
The above analysis suggests a straightforward procedure for experimentally determining the dynamic response of a structure, and the parameters that characterize it. We simply provide a force to our structure that varies sinusoidally at a particular frequency, w, with a defined (or measured) amplitude, fm. We then measure the steady state amplitude of the displacement fluctuations, xm, that force produces and the phase lag between the excitation and response, ym. This is then repeated for a range of frequencies. In the process we can discover the point where the phase lag reaches -90 degrees (the natural frequency) and the amplitude response is at a maximum (the resonant frequency), the phase and amplitude variations at low and high frequency, as well as the overall form of the response. It is exactly this type of scheme you can implement using the analog instrumentation available with this experiment.
These results are important experimentally because most of them suggest ways of measuring all three system parameters, m, b and k. One such scheme is:Think up some schemes for yourself.
The apparatus for this experiment can be described in three different groups, as suggested by Figure 3 : the structure, the excitation system, and the response system. Note that the excitation and response systems use much of the electronic instrumentation you have already been introduced to in instrumentation lab.
A. Beam Structure, General Items
The beam structure should be
mounted on the lab floor. (Unlike a desk, for example, the lab floor won't
vibrate significantly and thus become part of the dynamic system). The following
are its nominal characteristics:
L = 11.75 in., EI = 2,800 lb in.2, ρb go = 0.024 lb/s2.
Weights that may be added to the mass (in the form of large steel washers) are available. Calipers, a steel ruler, a tape measure, and a digital scale are available for you to record/check all dimensions/weights as you feel appropriate.
The structure is provided with the excitation and response systems described below.
B. Excitation System
Figure 5
is a functional diagram of the excitation system. The purpose of the excitation
system is to produce and measure the sinusoidally fluctuating force f(t)
= fmsin(ωt) used to shake the structure.
A BK Precision 4003A Function Generator is provided to produce the sinusoidal excitation signal. This is the same instrument you have already been introduced to in Instrumentation Lab. The generator should be set up to produce a sine wave in the 10 Hz range and always start with the amplitude knob turned all the way to 0, in the 0-20V. NOTE: you should never have to supply more than 5-6V from the function generator. ALWAYS monitor the signal amplitude so as not to damage the power amplifier or the shaker.
Remember that the sine wave will be produced at the 'Main' output socket.
To accurately measure the frequency or period of this signal (an important parameter, see Equations 1 or 2), use the provided Tektronix TBS 1052B oscilloscope.The TBS 1052B can also be used to display and measure the excitation signal. While you could use the BK Precision 2831E multimeter to measure the response root-mean-square (RMS) voltage, it is suggested to use it primarily to measure the output voltage of the DC power supply (used in the response system discussed in the next section). Both the oscilloscope and the multimeter provide a means to measure the voltage amplitude (recall that the RMS is 0.7071 of the amplitude) and thus, indirectly, the force amplitude fshaker applied by the electromechanical shaker. (However, note that the multimeter is not accurate for this purpose below about 10 Hz).
The shaker itself, a Brüel and Kjær LDSV203 permanent magnet shaker, requires a relatively large current, and thus cannot be driven by the voltage signal of the function generator itself. Instead, the connection is made through a power amplifier, which outputs a current that follows the excitation voltage. The sinusoidally fluctuating current drives the electrical coil of the shaker. The coil lies in the field of a permanent magnet contained in the steel cylinder, and thus the current results in the generation of an electromagnetic force. The shaker output force is measured using a PCB Piezoelectronics Model 482A21 unit driving a dynamic force sensor (PCB Model 208C01) with a range of +/- 44.5N. The sensor sensitivity is 100mV/N (with 5% uncertainty).
As discussed earlier, the force measured at the shaker location (at 17% of the beam length) needs to be corrected in order to be used with Equation 1. To do so, you can approximate the system as a cantilever beam. First, derive the expression for the deflection you would expect at the beam free end due to the force from the shaker located at 0.17L. Then derive the expression for the same deflection that would occur due to a point force applied at the free end (the assumption in Equation 1). By equating those two expression, you will obtain the relationship between the load generated by the shaker and the tip load that would create the same displacement. This relationship should be fm=0.041 fshaker for the setup described above.
Figure 6 shows the shaker mounted in the frame along with the force transducer. Note that the force sensor will be already connected to its control unit. BNC cables and connectors are provided to connect the rest of the excitation system.C. Response System
Figure 7
is a functional diagram of the response system. The purpose of the response
system is to sense and measure the displacement of the structure, x(t)
= xmsin(ωt+ψ), in response to the sinusoidal load.
The fluctuating position of the mass is measured using a non-contact device known as a proximitor that uses radio frequency waves and a steel target. The proximitor system is manufactured by the Bently Nevada Corporation and consists of a probe, type 330101-10-24-20-02-05, and a proximitor, type 330180-11-00, and a BK Precision 1673 power supply. When connected as shown in Figure 7, this sensor detects the gap between the probe tip and a steel target attached to the laboratory structure.
The proximitor requires -24 volts signal to operate . Make sure to connect your power supply correctly to produce the negative voltage needed.
If you are not sure, ask your TA for assistance.
Note: The proximitors also use a voltage divider on their output that divides the amplitude of the output signal by a factor of 2.
Therefore, to extract the actual displacement amplitude one needs to multiply the signal coming out of these proximitors by 2. This procedure applies TO ALL proximitors
The proximitor converts the -24 volts from the power supply into a radio frequency (RF) signal that is applied to the probe through cables. A coil within the probe tip radiates the RF signal into the surrounding area as a magnetic field. If there is no electrically conductive material (such as the steel target) close enough to intercept the magnetic field, then there is no power loss in the RF signal, and the voltage at the proximitor output terminal is maximum (about -14 volts). If a conductive target is close enough to the probe tip to intercept the magnetic field, then eddy currents are generated on the surface of the material, resulting in a power loss in the RF signal, and the negative voltage at the output terminal is reduced. If the conductive surface comes very close to the probe tip, then all of the RF power is absorbed, and the output voltage reduces to zero.
For a certain range of separations between the probe and the target, there is a linear relationship between gap and output voltage. Figure 8 is the calibration curve for the particular sensor used in this experiment with its steel target. The proximitor can be seen to vary linearly with the sensed distance with a slope of 200 millivolt/mil. In otherwords, a vibration of the beam with an amplitude of one thousandth of an inch would produce a fluctuating voltage signal from the proximitor output with an amplitude of 0.2V. Alternatively, if you measure a 1 V amplitude signal from the proximitor, that indicates an amplitude of the beam motion, xm = 1/0.2 = 5 thousandths of an inch.
As sketched on Figure 7, the probe is attached to an arm that extends from a magnetic base. The base is clamped magnetically to a steel plate that is bolted to the aluminum frame. The magnetic field of the base can be turned on or off with a large switch in the base, so the switch essentially attaches the base to or releases it from the steel plate. The probe tip must be positioned initially a certain gap distance away from the center of the steel target, as shown on Figure 7, and the face of the probe tip should be approximately parallel to the target surface (in other words, the axis of the probe should be perpendicular to the target surface). There are adjustment knobs on the arm connecting the probe to the magnetic base, but you should avoid using these if possible. The best way to position the probe relative to the target is to switch off the magnetic field of the base, then gently slide the magnetic base on the steel plate until you get the correct positioning, then switch on the magnetic base to clamp the entire assembly in the correct position.
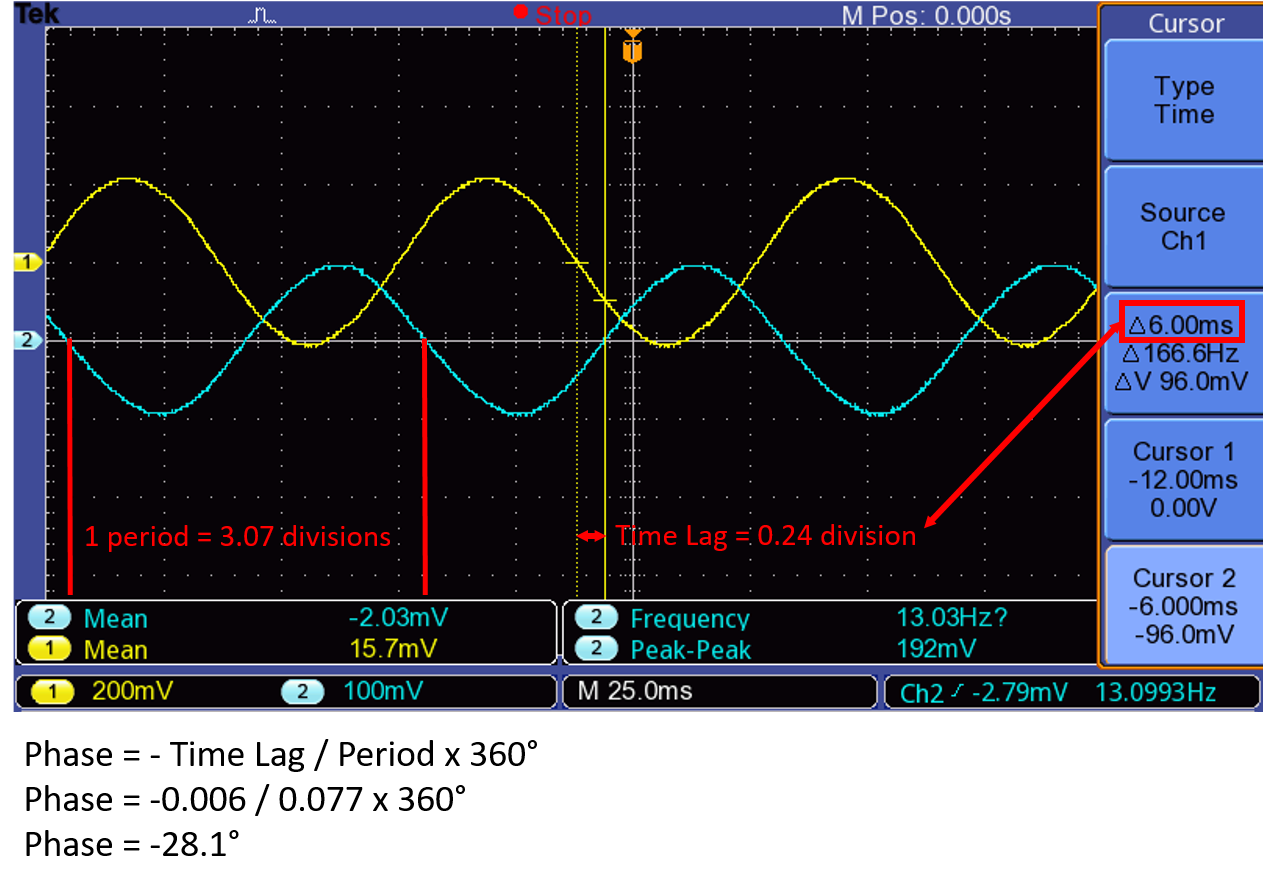
As shown on Figure 7, the proximitor output voltage is connected for observation and data recording to channel 2 of the Tektronix oscilloscope (and optionally to the BK Precision voltmeter) mentioned in the excitation section. Since the oscilloscope can display both the excitation and response signals simultaneously, it can be used to measure the phase response ψ. Figure 10 shows an example of how this can be done. Notice how both signals have been positioned symmetrically around a horizontal grid line, making it easier to see the time delay between the two signals as a time between two zero crossings.
This technique is fine in general (you can probably use the figure here
to make an estimate of its likely accuracy), but there is a much quicker way
of using the scope to tell when the phase lag is exactly 90o
and thus determining when the system is being excited at its natural frequency.
The technique is to use the X-Y capability of the scope, to plot the excitation
signal against the response signal in what is called a Lissajous figure. The
animations below are movies that show examples of Lissajous figures produced
for various phase angles. The elliptical figure in the top right hand corner of each
movie shows what you would see on the scope for the phase angle indicated
with the excitation signal connected to channel 1 of the scope (X) and the
response to channel 2 (Y).
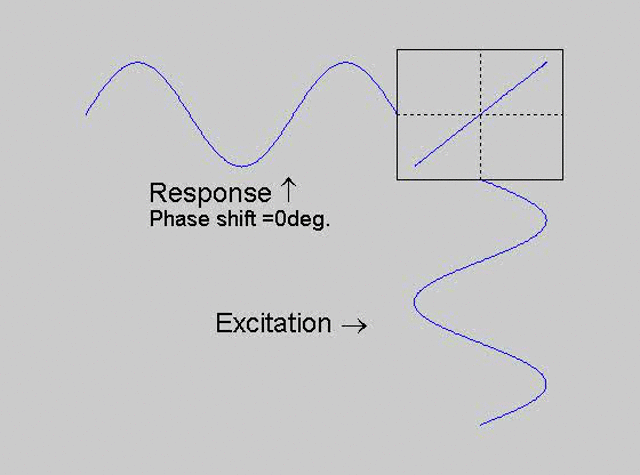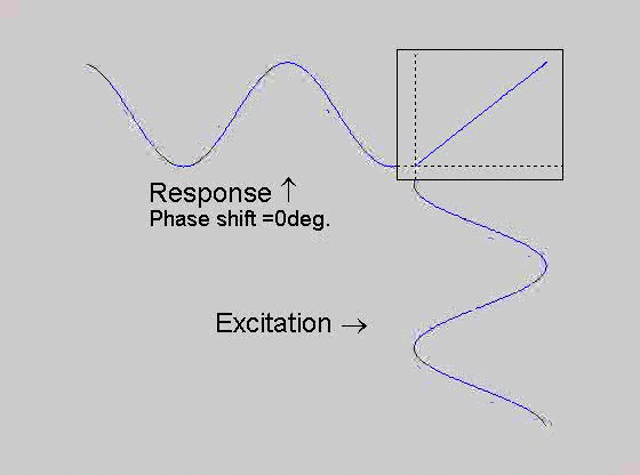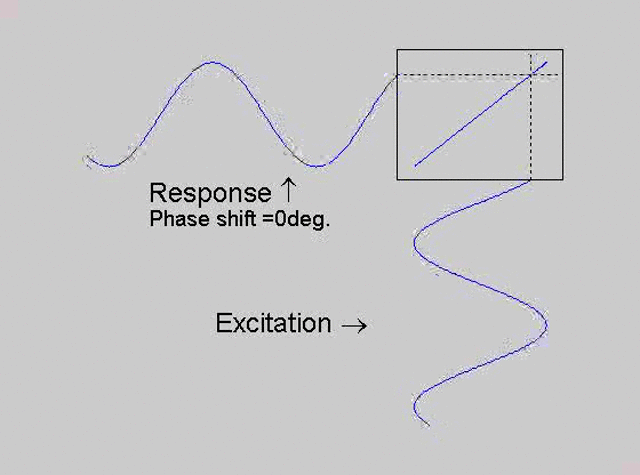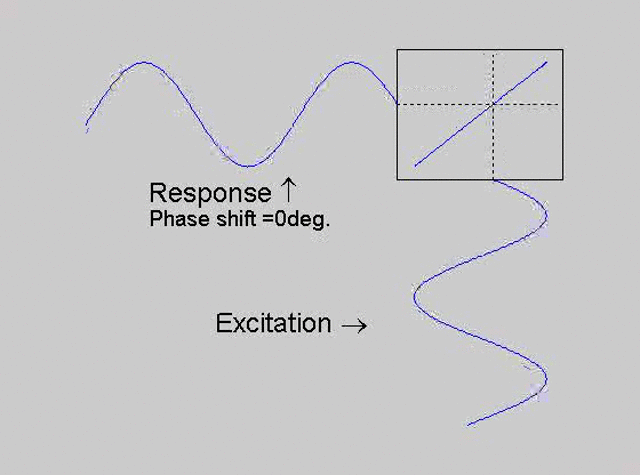
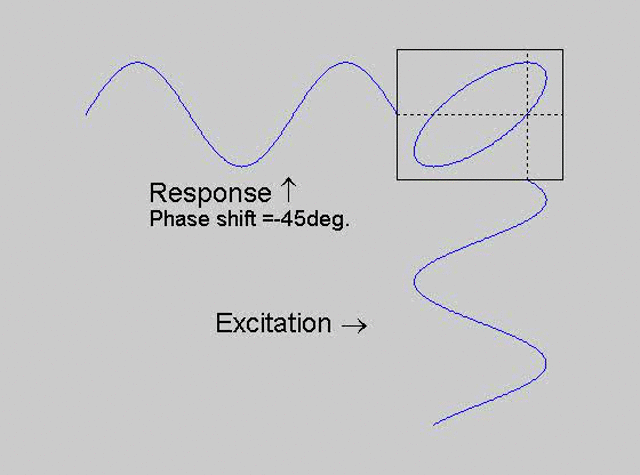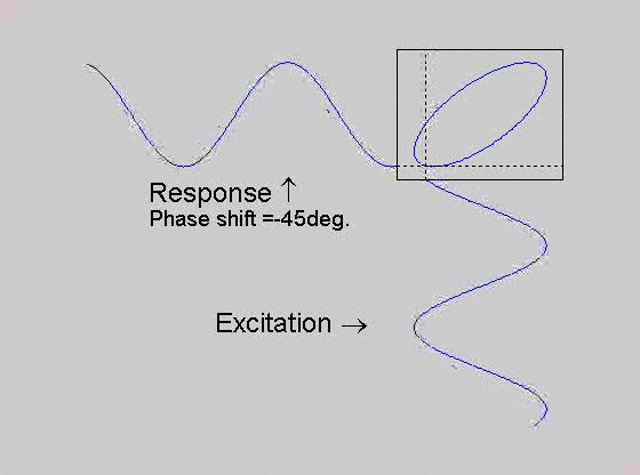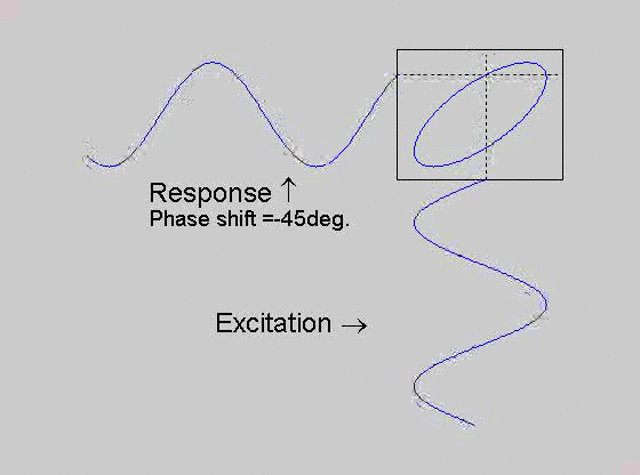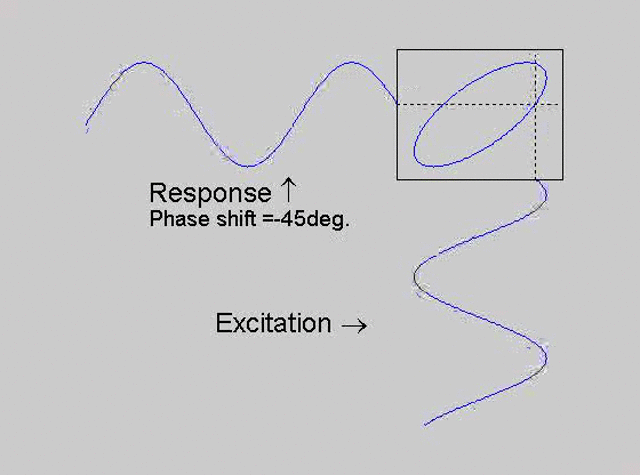
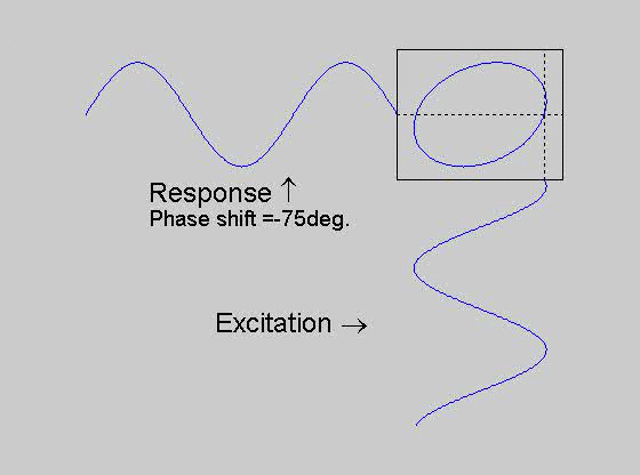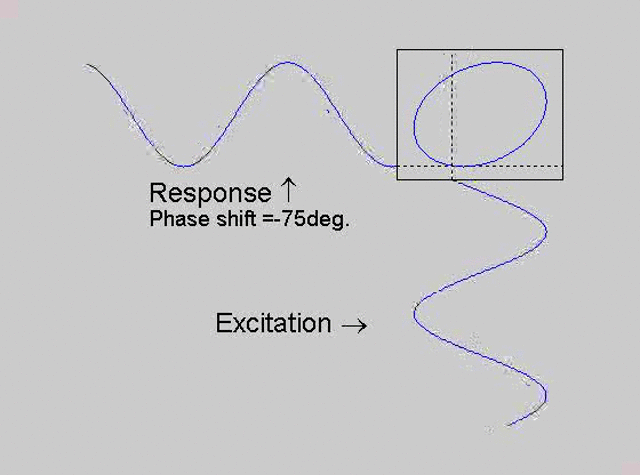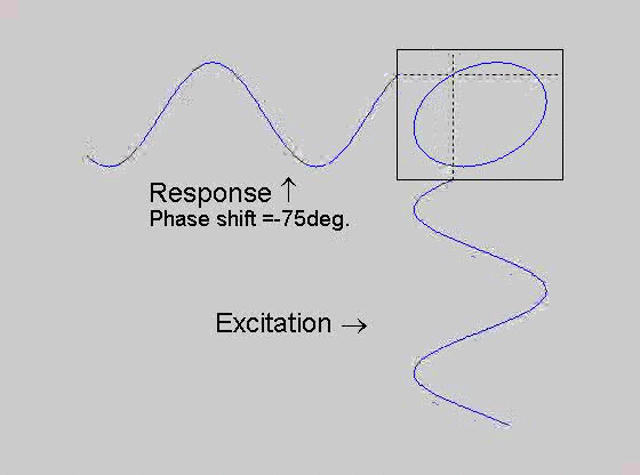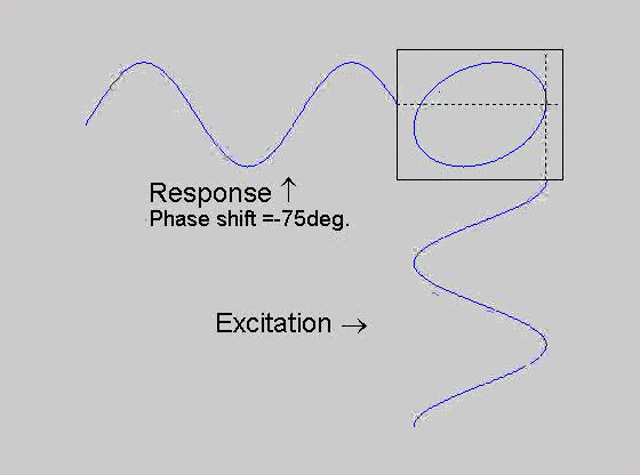
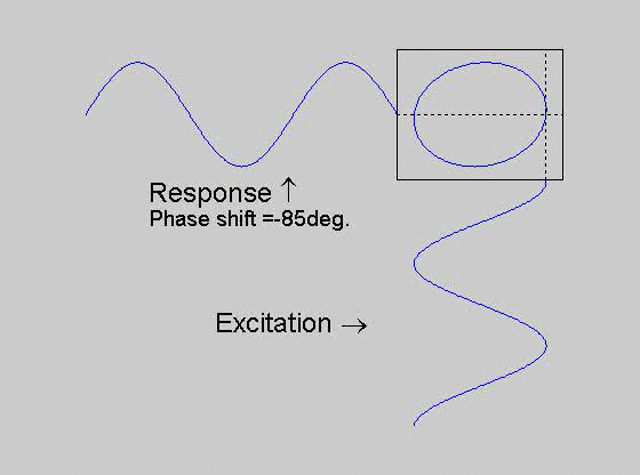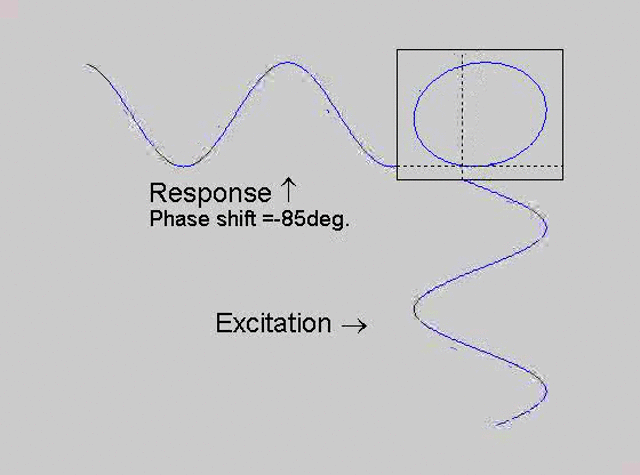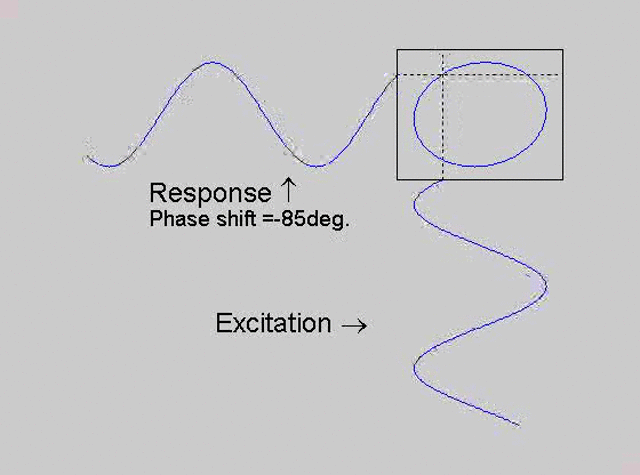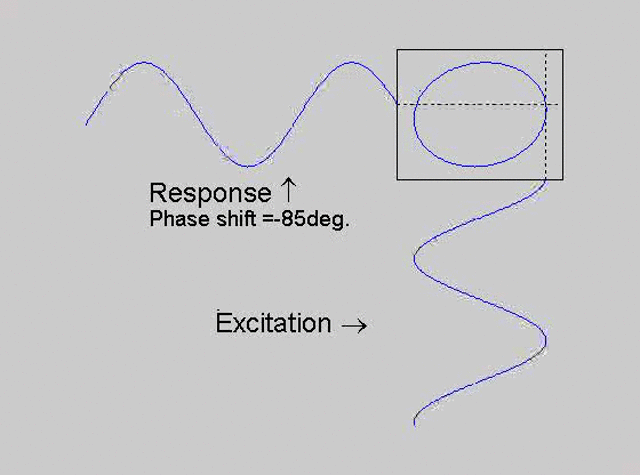
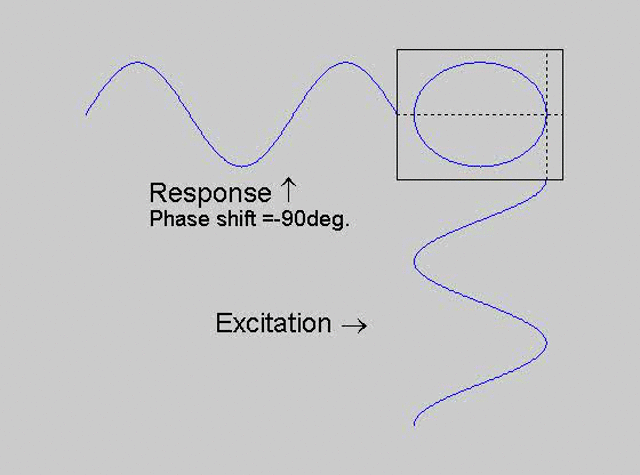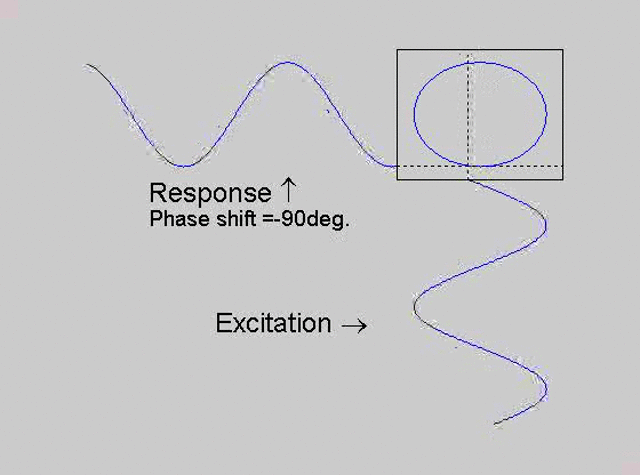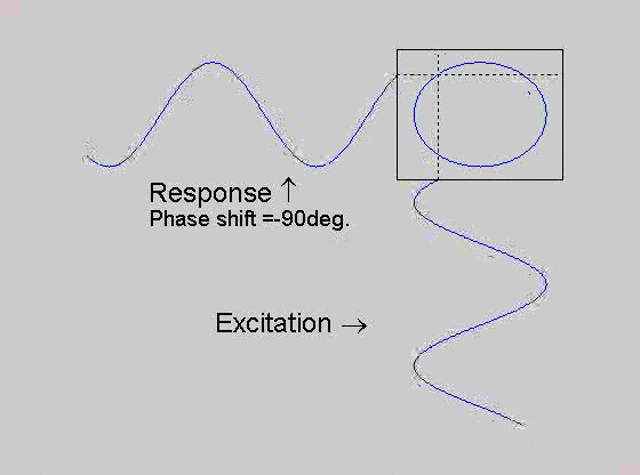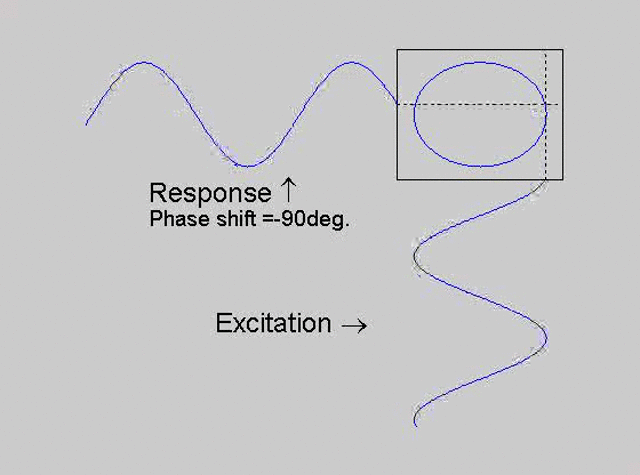
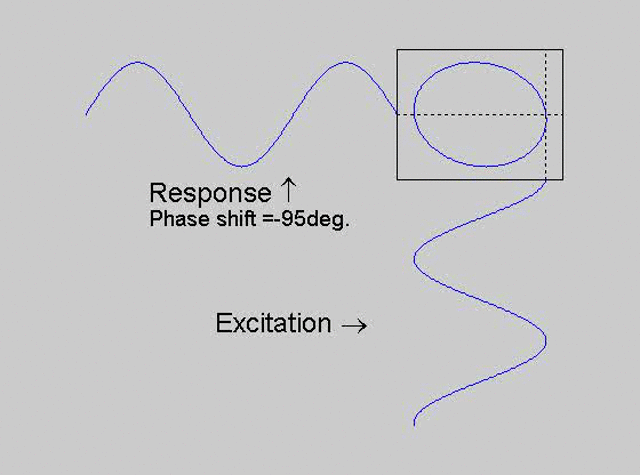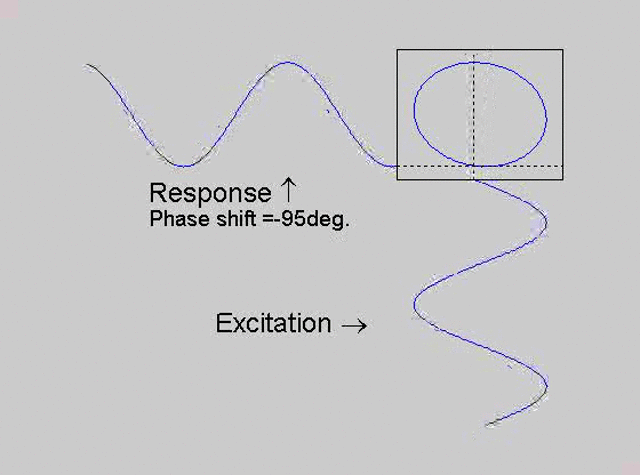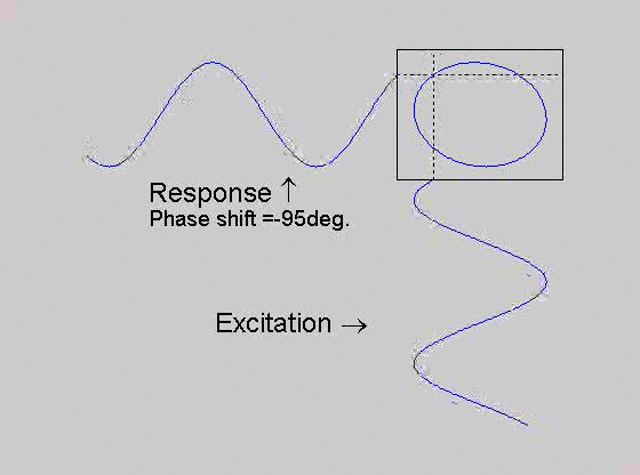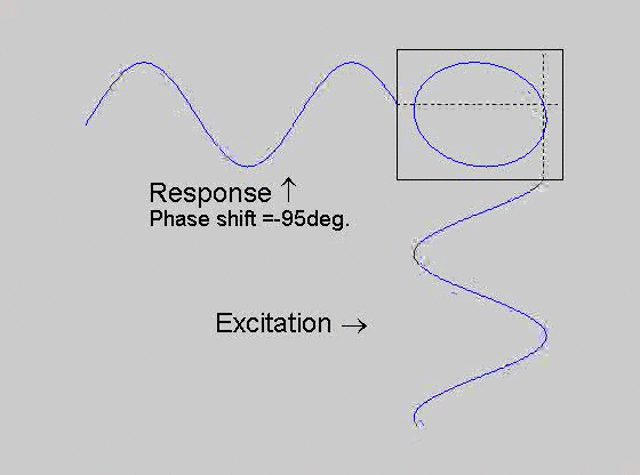
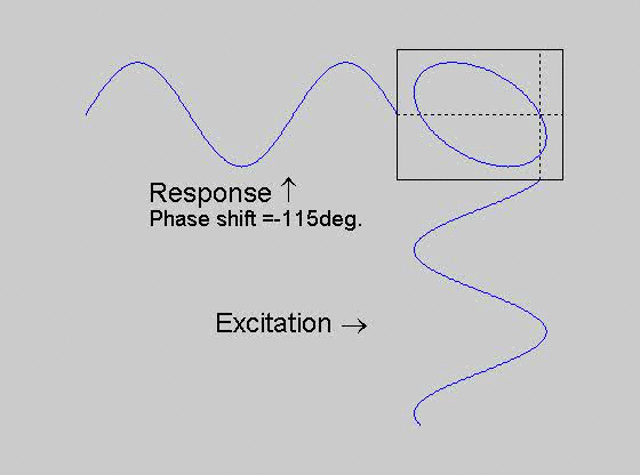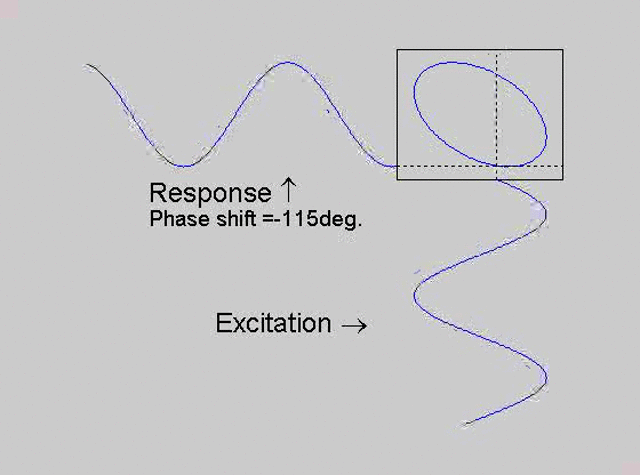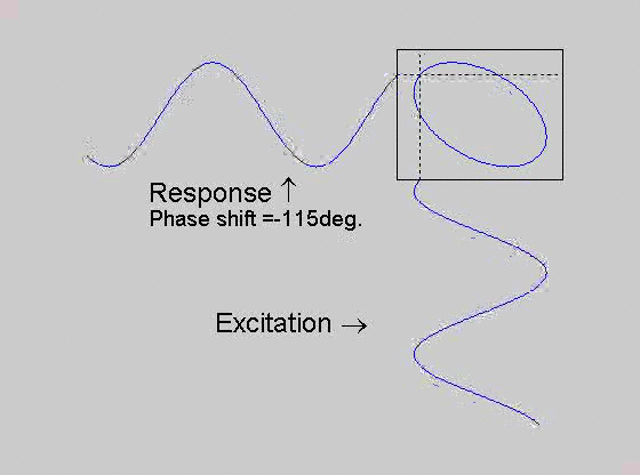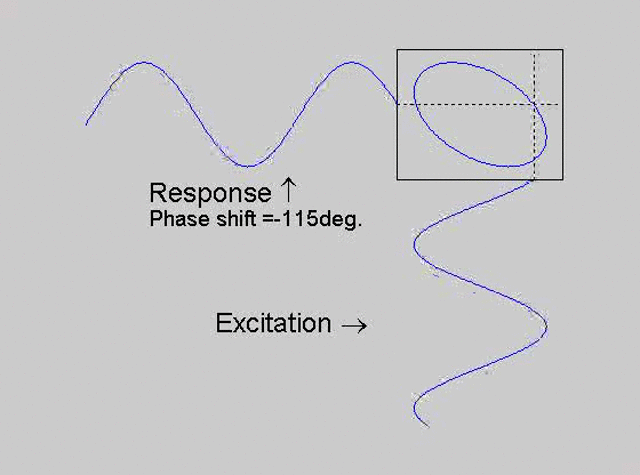
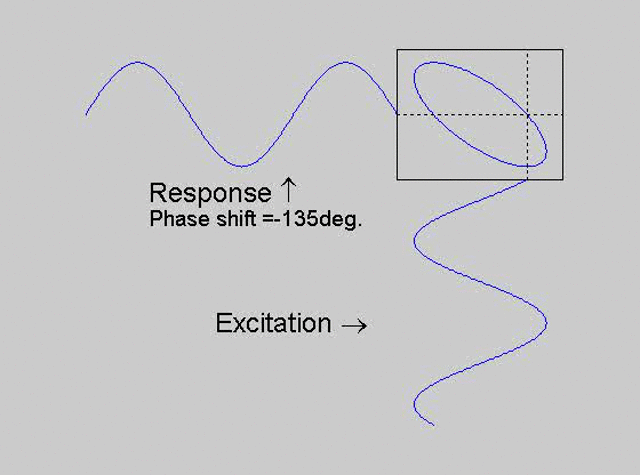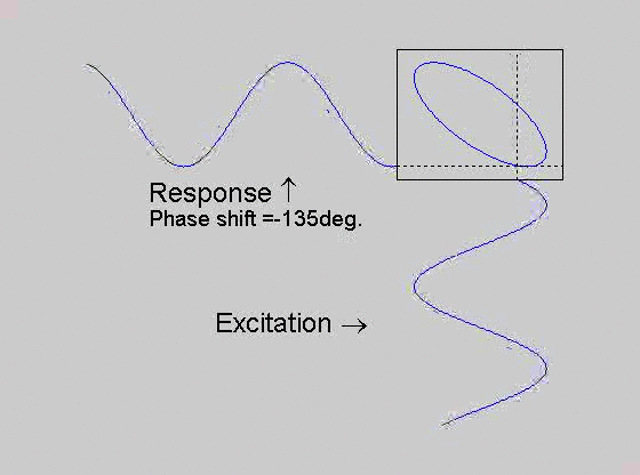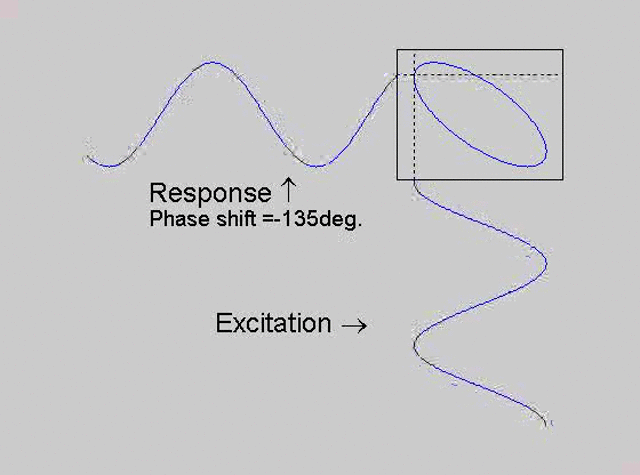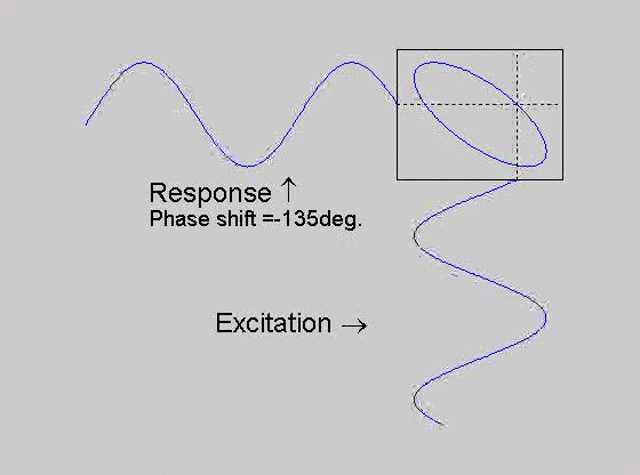
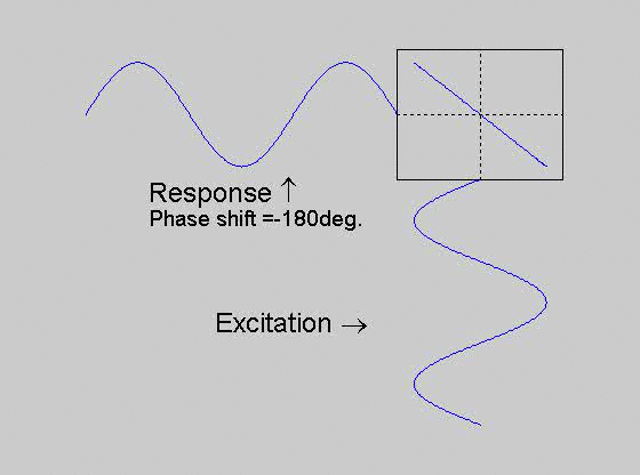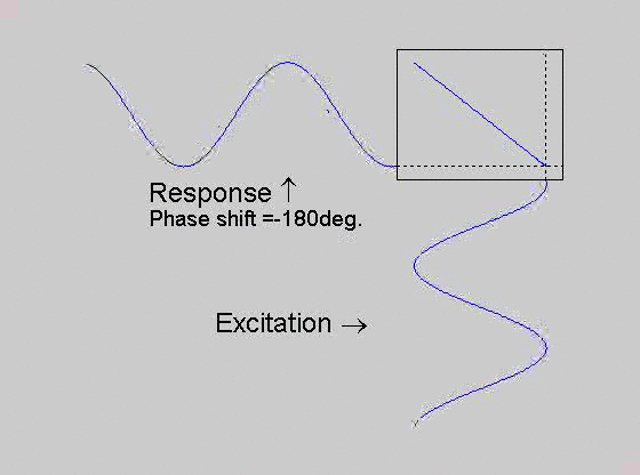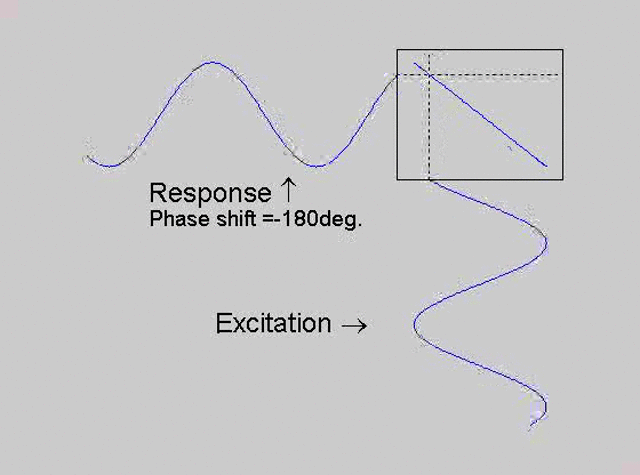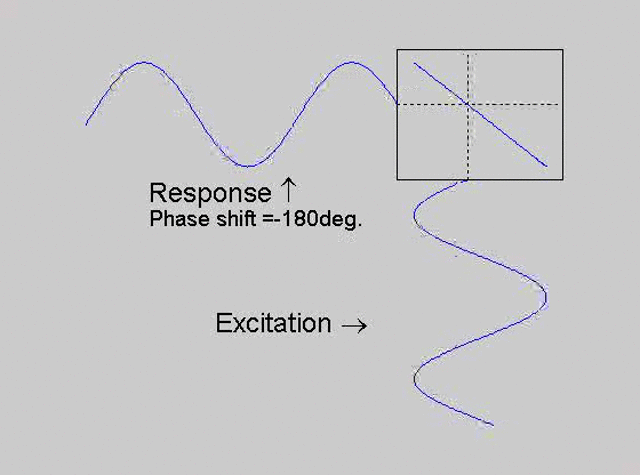
Note that only when the phase is exactly -90o are the major and minor axes of the Lissajous figure exactly vertical and horizontal. You may be able to use these movies, with some actual scope experience later to estimate the error in the phase angle, measured using this technique. The Lissajous figure is by far the quickest way of determining the natural frequency of a system, or the change in the natural frequency when the system is altered.
A. Getting familiar with the equipment
The following procedures are designed to help you get a feel for the beam
structure and its instrumentation. It is important that you get a hands-on feel of how to use the apparatus and what its capabilities and problems
are. Feel free to play with
the apparatus (but see item 2 concerning the power amplifier first). Don't
forget to record any results, thoughts, ideas, plans, photos or concerns
in the logbook. Be sure to ask your TA before turning any equipment on so he/she can come check your wiring.
Goal 1. Design, conduct, and implement a test or series of tests to estimate the three key parameters (total mass m, total damping b, total spring constant k) of the beam system using the scheme laid out at the end of Section 2,
Suggestions. It is really important to estimate the uncertainty in your results. You may be able to reduce this uncertainty by using extra measurements to get additional estimates, and averaging the answers. Keep careful documentation of what you do, why you do it, set up characteristics, expected results, unexpected results, analysis, photos and plots in the electronic log book as you proceed. Analysis as you go will help catch bad data or points before it's too late. It will be interesting to look at any differences between your estimates of the total mass and spring constant, and the nominal values that can be inferred from the information above. Measurements of the actual beam dimensions and imperfections may be useful in assessing the significance of any differences.Goal 2. Design, conduct, and implement a test, or series of tests, to investigate the extent to which the beam can be approximated as a linear system.
Suggestion. Measuring the entire response (phase and dynamic flexibility) characteristic is not such a bad way to proceed, but you may wish to focus your measurements on characteristics/regions of the response that are particularly identifiable with a linear system. Of course your assessment of the degree of validity of the linear response model will have to factor in your estimates of the accuracy of your results (e.g., comparing phase response measurements with theoretical estimates on a graph won't mean much without error bars on the phase measurements, as you won't know if the differences are significant or not). Plotting as you go will help catch bad data or points before it's too late. Keep careful documentation of what you do, why you do it, set up characteristics, expected results, unexpected results, analysis, photos and plots in the electronic log book as you proceed.Goal 3. Design, conduct and implement a test, or series of tests, to document the dependence of the natural frequency on the total mass, M, of the system, and compare with linear theory.
Suggestion. Don't forget the washers. The uncertainty on the natural frequency measurement, and on the original mass of the beam (and other factors) will be important factors if you really want to draw definitive conclusions from a comparison with the theory. Keep an eye out for uncontrolled parameters or beam behavior. Plotting/analysis as you go will help catch bad data or points before its too late. Keep careful documentation of what you do, why you do it, set up characteristics, expected results, unexpected results, analysis, photos and plots in the electronic log book as you proceed.
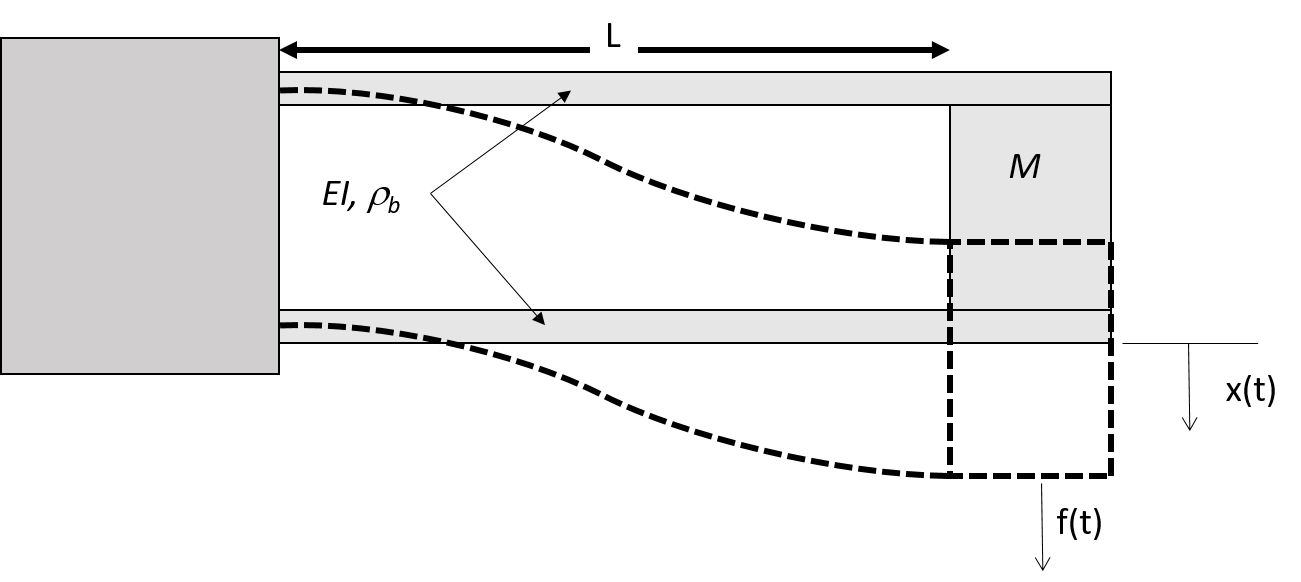
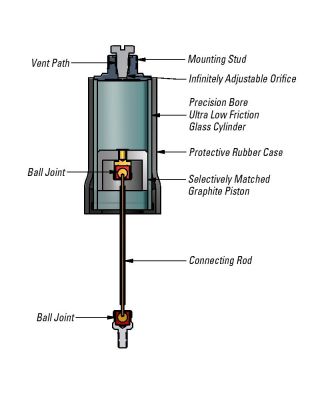
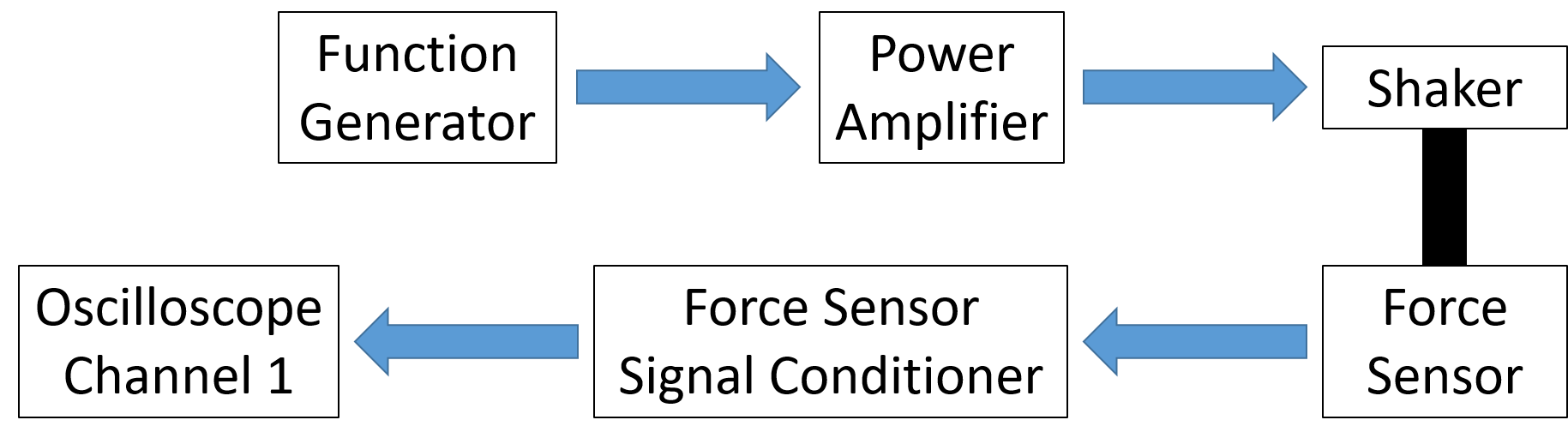
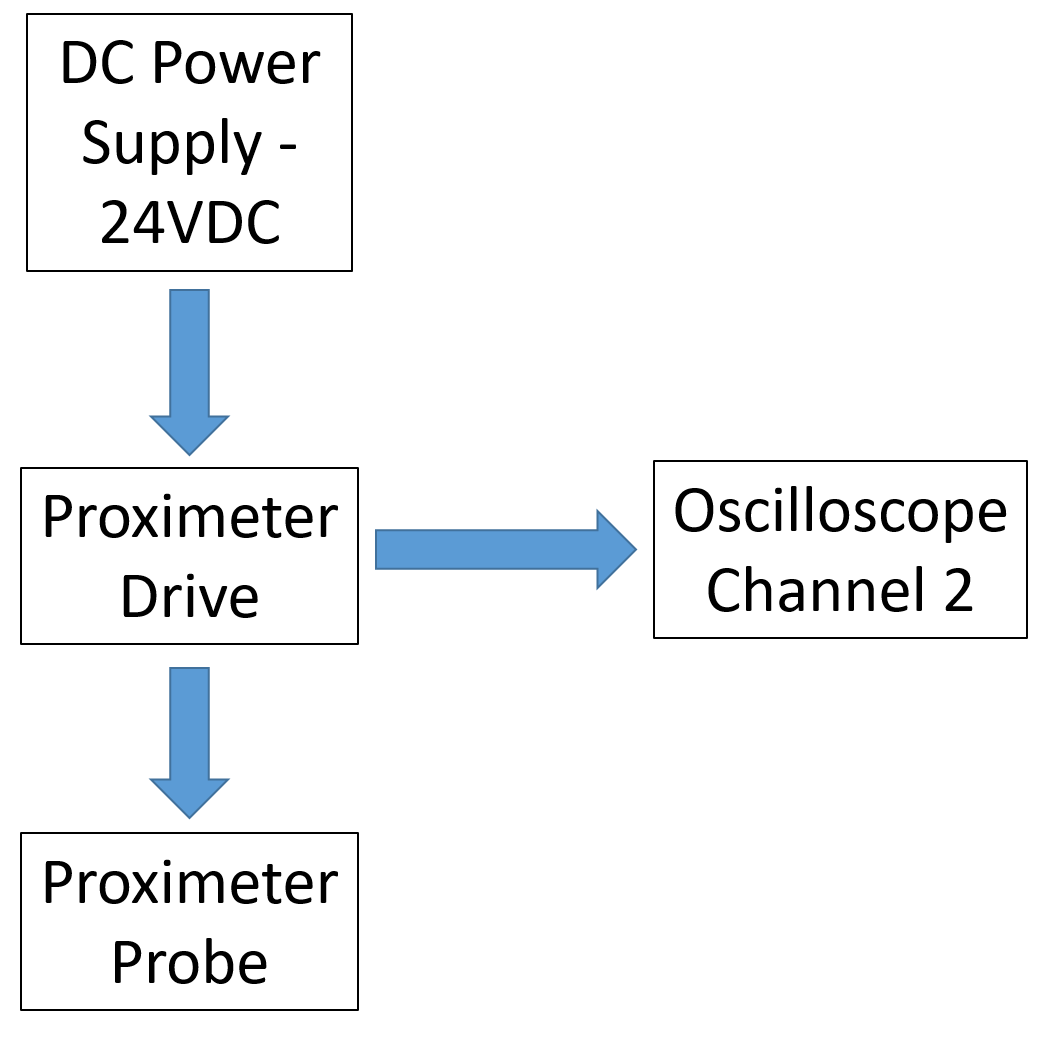
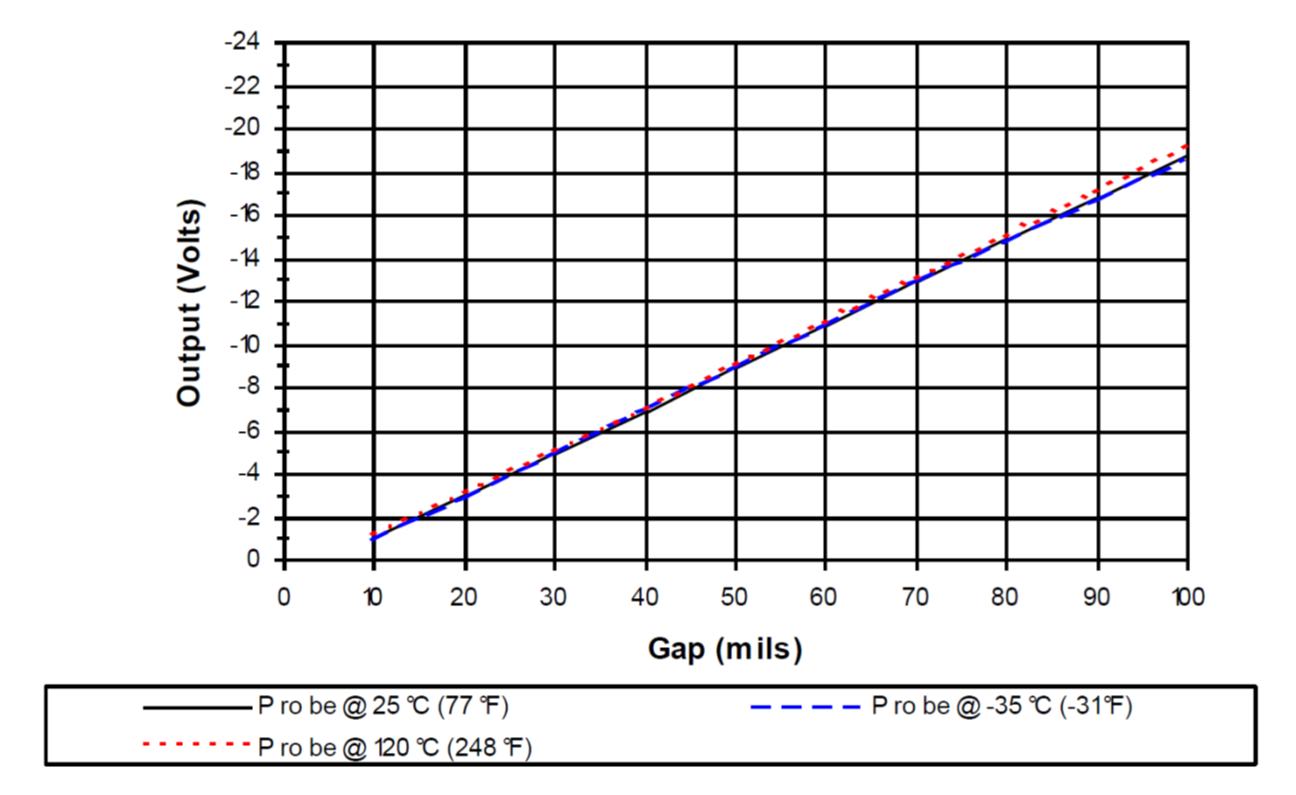
Figure 8. Proximity Sensor Calibration Curve
(from 3300 XL 8mm Proximity Transudcer System Manual (page 20))
